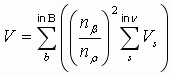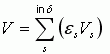Volume_integration

Let A be the set of samples s in the analysis domain for which Volume_integration is being calculated.

Then the volume of any one sample in A is defined as follows (see also About integration algorithms):

Where:

Vs	=	Volume of sample s (m3)
	=	Unit distance along the cruise track = 1 (m)
	=	Unit cross-sectional area across the cruise track = 1 (m2)
Δxp	=	Distance along the cruise track for ping p (m) = Vgp·Δtp where Vgp is available, and otherwise

Where:

Vgp = Vessel speed over ground at ping p (m/s)
Δtp = Pulse repetition interval for ping p (s)

Φp   = Bearing angle of the ping p (radians).
Note: This bearing angle is measured clockwise when viewed from above with 0 bearing in the direction of travel (direction of Vgp). The measure of bearing is however instrument (and mode) specific and translations are performed where required.

Δθb = Angular width of beam b (radians) = θ / (Nb)
Δθbv = Angular width of beam b in the V-mode ping of a target-locked pair (radians) = θ / (Nb)
Δθbh = Angular width of beam b in the H-mode ping of a target-locked pair (radians) = θ / (Nb)

Where:

θ   = Full sector angle of the respective ping (radians)
Nb = Number of beams in full sector of the respective ping (-)

rs = Range of sample s (m) = rminp + (ns+0.5)·Δrs

Where:

rminp = Minimum range for ping p (m)
ns     = zero based sample number measured from transducer (-)
Δrs   = Thickness of sample s in the range dimension (m) = (rmaxp– rminp)/ (Nsp)

Where:

rmaxp = Maximum range for ping p (m)
rminp = Minimum range for ping p (m)
Nsp   = Number of samples in ping p

Τp = Tilt angle of the ping p (radians), read from the data file for H- and S- mode and 0 in V-mode.

Τs = The effective Tilt angle of a sample s (radians), defined as follows:

if s is on an H-mode ping then Τs = Τp
if s is on a V-mode ping then Τs is calculated as (b + 0.5) × Δθbv

Where:

b = the number of the V-mode ping on which sample s lies (-)
Δθbv = as defined above (radians)

Note: The Single beam algorithm is used for integration of single beam data, and the remaining algorithms for integrating multibeam data. See About integration algorithms for more information on the various algorithms.

Then the integration volume is determined as:

Where:

V	=	the integration volume, Volume_integration (m3)
	=			0 if sample s is not in the analysis domain
				1 otherwise, including below threshold data.
Vs	=	Volume of sample s (m3) - as defined above
δ	=	the set of samples in the analysis domain.
Β	=	the set of beams in the analysis domain and on the H-mode ping of a target-locked pair.
β	=	the set of samples in the analysis domain and on the beam b of the H-mode ping of a target- locked pair.
ρ	=	the set of samples in the analysis domain and on the beam i of the H-mode ping of a target- locked pair,       where i is the number of the reference beam,       which is that beam which the V-mode ping of the target-locked pair intersects.
ν	=	the set of samples in the analysis domain and on the V-mode ping of a target-locked pair.
nβ	=	the number of samples in the set β
nρ	=	the number of samples in the set ρ

Notes

1. Volume_integration is NOT calculated whenever 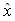is used. The sample volume, Vs may still be calculated for use in the calculation of Sv_mean but any calculation of Vs by using 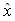is not considered useful for the purposes of volume or biomass estimation. If Volume_integration is not calculated for this reason, a special value will be provided instead. The following variables depend upon Volume_integration and cannot be calculated if Volume_integration is not calculated:
   • Fish_weight
   • Fish_number
   • N_sigma_bs

See also

Density_number
Density_weight
Fish_number
Fish_weight
N_sigma_bs